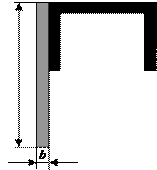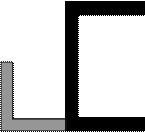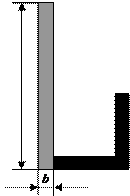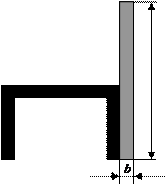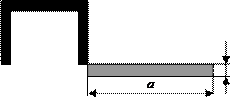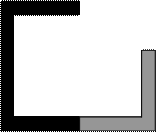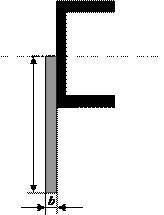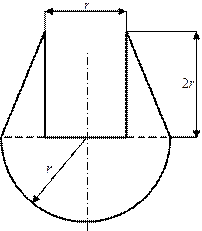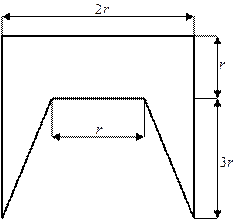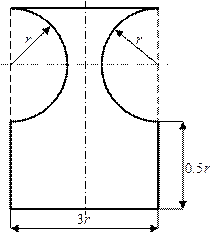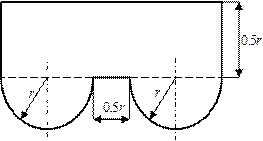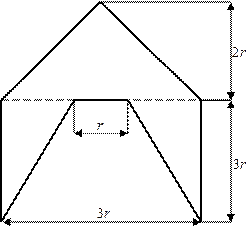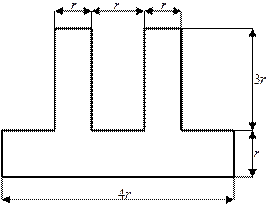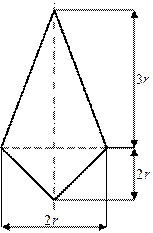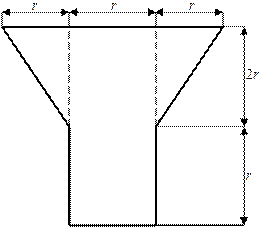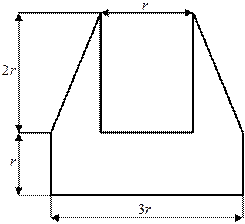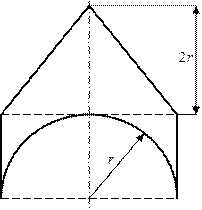Главная
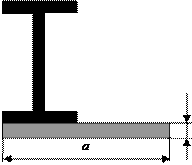
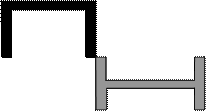
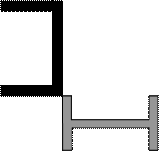
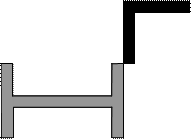
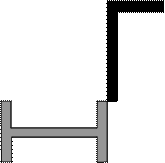
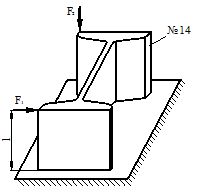
Задача 1. Действие сил в разных плоскостях
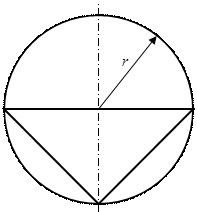
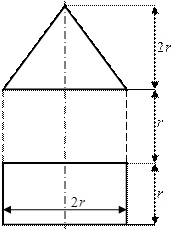
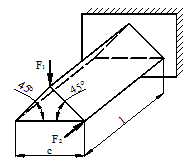
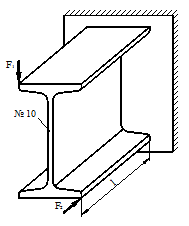
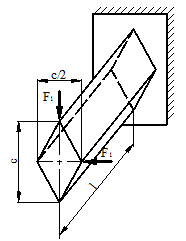
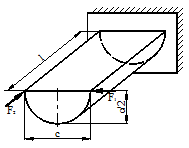
Для схемы, показанной на рис.1 необходимо:
1) Вычертить ее в произвольном
масштабе.
2) Для произвольного поперечного
сечения стержня записать уравнения внутренних силовых факторов.
3) Построить эпюры внутренних
силовых факторов.
Данные взять из табл.1.
Таблица 1
|
Номер cтроки |
Схема по рис.1 |
l, м |
c, м |
F1, кН |
F2, кН |
|
01 |
1 |
1,1 |
0,2 |
10 |
25 |
|
02 |
2 |
1,2 |
0,3 |
15 |
30 |
|
03 |
3 |
1,3 |
0,4 |
20 |
15 |
|
04 |
4 |
1,4 |
0,5 |
25 |
20 |
|
05 |
5 |
1,5 |
0,6 |
30 |
25 |
|
06 |
6 |
1,6 |
0,7 |
10 |
15 |
|
07 |
7 |
1,7 |
0,8 |
15 |
20 |
|
08 |
8 |
1,8 |
0,9 |
20 |
30 |
|
09 |
9 |
1,9 |
0,4 |
25 |
10 |
|
10 |
10 |
2,0 |
0,7 |
30 |
20 |
|
11 |
11 |
1,3 |
0,4 |
20 |
23 |
|
12 |
12 |
1,4 |
0,5 |
25 |
24 |
|
13 |
13 |
1,5 |
0,6 |
30 |
25 |
|
14 |
14 |
1,6 |
0,7 |
10 |
26 |
|
15 |
15 |
1,7 |
0,8 |
15 |
27 |
|
16 |
16 |
1,8 |
0,9 |
20 |
28 |
|
17 |
17 |
1,6 |
0,4 |
25 |
29 |
|
18 |
18 |
1,7 |
0,8 |
25 |
21 |
|
19 |
19 |
1,8 |
0,9 |
30 |
22 |
|
20 |
20 |
1,9 |
0,4 |
10 |
23 |
|
21 |
21 |
2,0 |
0,7 |
15 |
24 |
|
22 |
22 |
1,3 |
0,4 |
20 |
25 |
|
23 |
23 |
1,4 |
0,5 |
25 |
26 |
|
24 |
24 |
1,5 |
0,6 |
30 |
27 |
|
25 |
25 |
1,6 |
0,7 |
20 |
28 |
|
26 |
26 |
1,7 |
0,2 |
25 |
29 |
|
27 |
27 |
1,8 |
0,3 |
30 |
30 |
|
28 |
28 |
2,0 |
0,4 |
10 |
23 |
|
29 |
29 |
1,3 |
0,5 |
15 |
24 |
|
30 |
30 |
1,4 |
0,6 |
20 |
25 |
|
31 |
31 |
1,5 |
0,7 |
25 |
26 |
|
32 |
32 |
1,6 |
0,8 |
70 |
27 |
|
33 |
33 |
1,7 |
0,9 |
80 |
28 |
|
34 |
34 |
1,4 |
0,4 |
90 |
29 |
|
35 |
35 |
1,5 |
0,7 |
15 |
23 |
|
36 |
36 |
1,6 |
0,5 |
20 |
24 |
|
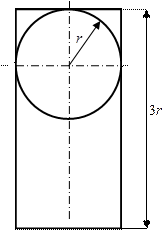
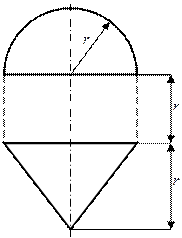
|
а |
б |
в |
г |
а |
1 схема 2 схема
3 схема
4 схема 5
схема 6 схема
7 схема 8 схема 9 схема
10 схема 11 схема 12 схема


13 схема 14 схема 15 схема



16 схема 17 схема 18 схема



19 схема 20 схема 21 схема



22 схема 23 схема 24 схема



25 схема 26 схема 27 схема



28 схема 29
схема 30 схема



31 схема 32 схема 33 схема



34 схема
35 схема 36 схема



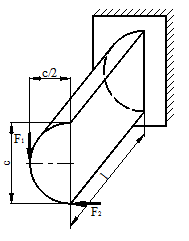
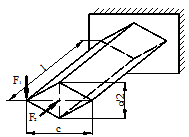
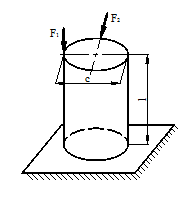
Рис.1
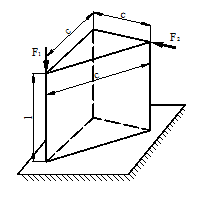
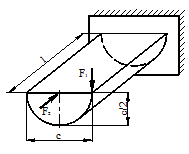
Задача 2. Действие сил в разных плоскостях
Консольный стержень (рис.2) нагружен сосредоточенными
силами F1, F2 и F3. Определить при помощи метода сечений внутренние
силовые факторы в сечении, удаленном на расстояние l от свободного конца стержня.
Данные взять из табл.2 и рис.2.
Примечание. В таблице знак минус показывает, что соответствующая
нагрузка должна быть приложена на расчетной схеме в направлении, противоположном
указанному на рисунке.
Таблица 2
|
Номер cтроки |
Схема по рис.2 |
l/a |
F1/P |
F2/P |
F3/P |
|
01 |
I |
10 |
4 |
1 |
3 |
|
02 |
II |
4 |
–1 |
3 |
2 |
|
03 |
III |
8 |
2 |
–4 |
1 |
|
04 |
IV |
16 |
3 |
2 |
–4 |
|
05 |
V |
10 |
1 |
–2 |
1 |
|
06 |
VI |
12 |
–1 |
1 |
3 |
|
07 |
VII |
16 |
2 |
3 |
–1 |
|
08 |
VIII |
20 |
–2 |
4 |
2 |
|
09 |
IX |
14 |
2 |
–4 |
4 |
|
10 |
X |
12 |
–4 |
1 |
–2 |
|
11 |
I |
10 |
4 |
1 |
3 |
|
12 |
II |
4 |
–1 |
3 |
2 |
|
13 |
III |
8 |
2 |
–4 |
1 |
|
14 |
IV |
16 |
3 |
2 |
–4 |
|
15 |
V |
10 |
1 |
–2 |
1 |
|
16 |
VI |
12 |
–1 |
1 |
3 |
|
17 |
VII |
16 |
2 |
3 |
–1 |
|
18 |
VIII |
20 |
–2 |
4 |
2 |
|
19 |
IX |
14 |
2 |
–4 |
4 |
|
20 |
X |
12 |
–4 |
1 |
–2 |
|
21 |
I |
10 |
4 |
1 |
3 |
|
22 |
II |
4 |
–1 |
3 |
2 |
|
23 |
III |
8 |
2 |
–4 |
1 |
|
24 |
IV |
16 |
3 |
2 |
–4 |
|
25 |
V |
10 |
1 |
–2 |
1 |
|
26 |
VI |
12 |
–1 |
1 |
3 |
|
27 |
VII |
16 |
2 |
3 |
–1 |
|
28 |
VIII |
20 |
–2 |
4 |
2 |
|
29 |
IX |
14 |
2 |
–4 |
4 |
|
30 |
X |
12 |
–4 |
1 |
–2 |
|
31 |
I |
10 |
4 |
1 |
3 |
|
32 |
II |
4 |
–1 |
3 |
2 |
|
33 |
III |
8 |
2 |
–4 |
1 |
|
34 |
IV |
16 |
3 |
2 |
–4 |
|
35 |
V |
10 |
1 |
–2 |
1 |
|
36 |
VI |
12 |
–1 |
1 |
3 |
|
|
в |
б |
а |
г |
в |
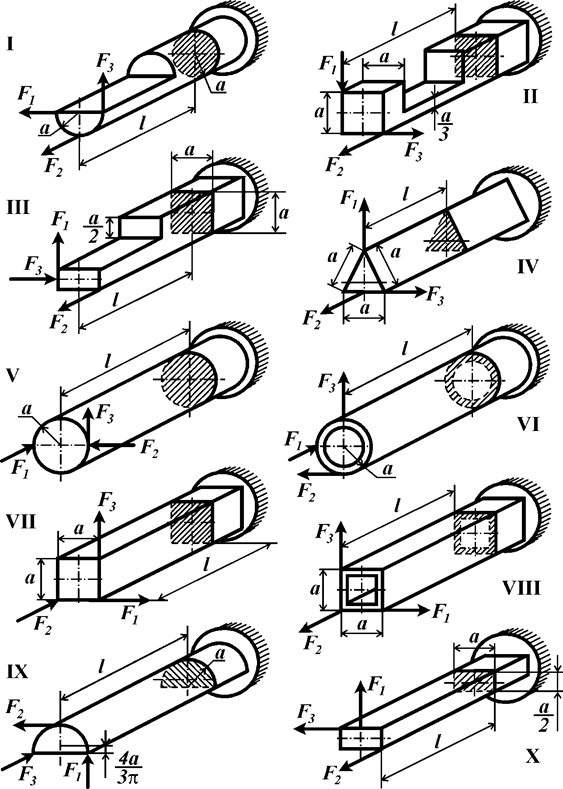
Рис.2
Задача 3. Расчет шарнирной балки,
подверженной косому изгибу
Стальная балка (рис.3) нагружена силами F1 и F2.
Требуется:
1. для опасного поперечного сечения балки определить положение
нейтральной линии;
2. из расчета на прочность по наибольшим напряжениям
определить допустимое значение параметра нагрузки P.
Принять: l=50 см, [n]=2,0, σт для
каждой марки стали брать по справочным данным.
Остальные данные взять из табл.3 и рис.3.
Таблица 3
|
Номер cтроки |
Схема по рис.3 |
Тип сечения |
l1 /l |
l2 /l |
t, мм |
h/t |
b/t |
F1/P |
F2/P |
Материал |
|
01 |
I |
1 |
1 |
2 |
8 |
5 |
3 |
–3 |
–1 |
Сталь 20 |
|
02 |
II |
2 |
2 |
1 |
9 |
6 |
4 |
2 |
–2 |
Сталь 3 |
|
03 |
I |
3 |
1 |
2 |
10 |
7 |
5 |
1 |
3 |
Сталь 4 |
|
04 |
II |
4 |
2 |
1 |
5 |
8 |
6 |
–3 |
1 |
Сталь 5 |
|
05 |
I |
5 |
1 |
2 |
6 |
5 |
4 |
–2 |
–2 |
Сталь 40 |
|
06 |
II |
6 |
2 |
1 |
7 |
6 |
5 |
1 |
3 |
Сталь 45 |
|
07 |
I |
1 |
1 |
2 |
8 |
7 |
6 |
3 |
1 |
20ХН |
|
08 |
II |
2 |
2 |
1 |
10 |
8 |
7 |
–2 |
–2 |
40Х |
|
09 |
I |
3 |
1 |
2 |
5 |
5 |
4 |
–1 |
–3 |
40ХН |
|
10 |
II |
4 |
2 |
1 |
7 |
6 |
3 |
2 |
1 |
12ХН3А |
|
11 |
I |
1 |
1 |
2 |
8 |
5 |
3 |
–3 |
–1 |
Сталь 20 |
|
12 |
II |
2 |
2 |
1 |
9 |
6 |
4 |
2 |
–2 |
Сталь 3 |
|
13 |
I |
3 |
1 |
2 |
10 |
7 |
5 |
1 |
3 |
Сталь 4 |
|
14 |
II |
4 |
2 |
1 |
5 |
8 |
6 |
–3 |
1 |
Сталь 5 |
|
15 |
I |
5 |
1 |
2 |
6 |
5 |
4 |
–2 |
–2 |
Сталь 40 |
|
16 |
II |
6 |
2 |
1 |
7 |
6 |
5 |
1 |
3 |
Сталь 45 |
|
17 |
I |
1 |
1 |
2 |
8 |
7 |
6 |
3 |
1 |
20ХН |
|
18 |
II |
2 |
2 |
1 |
10 |
8 |
7 |
–2 |
–2 |
40Х |
|
19 |
I |
3 |
1 |
2 |
5 |
5 |
4 |
–1 |
–3 |
40ХН |
|
20 |
II |
4 |
2 |
1 |
7 |
6 |
3 |
2 |
1 |
12ХН3А |
|
21 |
I |
1 |
1 |
2 |
8 |
5 |
3 |
–3 |
–1 |
Сталь 20 |
|
22 |
II |
2 |
2 |
1 |
9 |
6 |
4 |
2 |
–2 |
Сталь 3 |
|
23 |
I |
3 |
1 |
2 |
10 |
7 |
5 |
1 |
3 |
Сталь 4 |
|
24 |
II |
4 |
2 |
1 |
5 |
8 |
6 |
–3 |
1 |
Сталь 5 |
|
25 |
I |
5 |
1 |
2 |
6 |
5 |
4 |
–2 |
–2 |
Сталь 40 |
|
26 |
II |
6 |
2 |
1 |
7 |
6 |
5 |
1 |
3 |
Сталь 45 |
|
27 |
I |
1 |
1 |
2 |
8 |
7 |
6 |
3 |
1 |
20ХН |
|
28 |
II |
2 |
2 |
1 |
10 |
8 |
7 |
–2 |
–2 |
40Х |
|
29 |
I |
3 |
1 |
2 |
5 |
5 |
4 |
–1 |
–3 |
40ХН |
|
30 |
II |
4 |
2 |
1 |
7 |
6 |
3 |
2 |
1 |
12ХН3А |
|
31 |
I |
1 |
1 |
2 |
8 |
5 |
3 |
–3 |
–1 |
Сталь 20 |
|
32 |
II |
2 |
2 |
1 |
9 |
6 |
4 |
2 |
–2 |
Сталь 3 |
|
33 |
I |
3 |
1 |
2 |
10 |
7 |
5 |
1 |
3 |
Сталь 4 |
|
34 |
II |
4 |
2 |
1 |
5 |
8 |
6 |
–3 |
1 |
Сталь 5 |
|
35 |
I |
5 |
1 |
2 |
6 |
5 |
4 |
–2 |
–2 |
Сталь 40 |
|
36 |
II |
6 |
2 |
1 |
7 |
6 |
5 |
1 |
3 |
Сталь 45 |
|
|
а |
б |
б |
а |
г |
в |
г |
в |
а |
б |
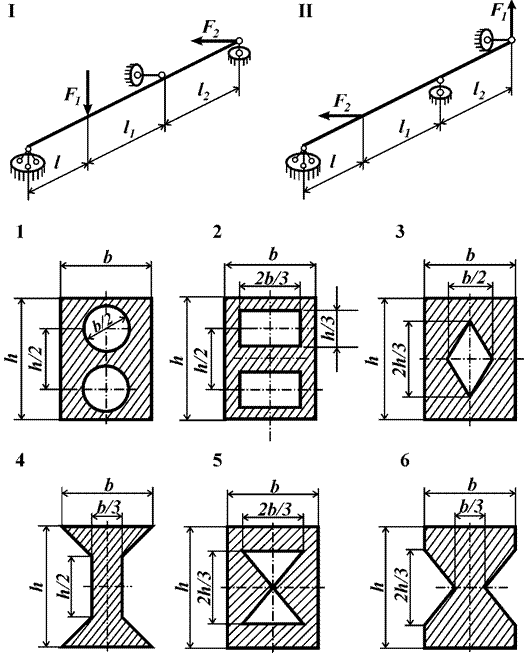
Рис.3
Задача 4. Расчет консольной балки,
подверженной косому изгибу. Определение запаса прочности.
Стальная консольная балка (рис.4) нагружена силами F1 и F2.
Требуется:
1. определить положение нейтральной линии для опасного
сечения;
2. определить запас прочности балки.
Принять: σТ=420 МПа; l=30 см.
Остальные данные взять из табл.4 и рис.4.
Таблица 4
|
Номер cтроки |
Схема по рис.4 |
Тип сечения |
l1 /l |
t, мм |
h/t |
b/t |
F1/P |
F2/P |
P, кН |
|
01 |
I |
1 |
1 |
6 |
12 |
2 |
3 |
–1 |
0,5 |
|
02 |
II |
2 |
2 |
8 |
9 |
3 |
–2 |
2 |
0,6 |
|
03 |
I |
2 |
3 |
10 |
6 |
4 |
1 |
3 |
0,7 |
|
04 |
II |
1 |
1 |
12 |
15 |
2 |
–3 |
1 |
0,8 |
|
05 |
I |
1 |
2 |
6 |
12 |
3 |
2 |
–2 |
0,9 |
|
06 |
II |
2 |
3 |
8 |
6 |
4 |
–1 |
3 |
1,0 |
|
07 |
I |
2 |
1 |
10 |
6 |
2 |
3 |
–1 |
0,5 |
|
08 |
II |
1 |
2 |
12 |
15 |
3 |
–2 |
–2 |
0,6 |
|
09 |
I |
1 |
3 |
9 |
9 |
4 |
1 |
–3 |
0,7 |
|
10 |
II |
2 |
1 |
7 |
6 |
4 |
–2 |
1 |
0,8 |
|
11 |
I |
2 |
1 |
6 |
12 |
2 |
3 |
–1 |
0,5 |
|
12 |
II |
1 |
2 |
8 |
9 |
3 |
–2 |
2 |
0,6 |
|
13 |
I |
1 |
3 |
10 |
6 |
4 |
1 |
3 |
0,7 |
|
14 |
II |
2 |
1 |
12 |
15 |
2 |
–3 |
1 |
0,8 |
|
15 |
I |
2 |
2 |
6 |
12 |
3 |
2 |
–2 |
0,9 |
|
16 |
II |
1 |
3 |
8 |
6 |
4 |
–1 |
3 |
1,0 |
|
17 |
I |
1 |
1 |
10 |
6 |
2 |
3 |
–1 |
0,5 |
|
18 |
II |
2 |
2 |
12 |
15 |
3 |
–2 |
–2 |
0,6 |
|
19 |
I |
2 |
3 |
9 |
9 |
4 |
1 |
–3 |
0,7 |
|
20 |
II |
1 |
1 |
7 |
6 |
4 |
–2 |
1 |
0,8 |
|
21 |
I |
1 |
1 |
6 |
12 |
2 |
3 |
–1 |
0,5 |
|
22 |
II |
2 |
2 |
8 |
9 |
3 |
–2 |
2 |
0,6 |
|
23 |
I |
2 |
3 |
10 |
6 |
4 |
1 |
3 |
0,7 |
|
24 |
II |
1 |
1 |
12 |
15 |
2 |
–3 |
1 |
0,8 |
|
25 |
I |
1 |
2 |
6 |
12 |
3 |
2 |
–2 |
0,9 |
|
26 |
II |
2 |
3 |
8 |
6 |
4 |
–1 |
3 |
1,0 |
|
27 |
I |
2 |
1 |
10 |
6 |
2 |
3 |
–1 |
0,5 |
|
28 |
II |
1 |
2 |
12 |
15 |
3 |
–2 |
–2 |
0,6 |
|
29 |
I |
1 |
3 |
9 |
9 |
4 |
1 |
–3 |
0,7 |
|
30 |
II |
2 |
1 |
7 |
6 |
4 |
–2 |
1 |
0,8 |
|
31 |
I |
2 |
1 |
6 |
12 |
2 |
3 |
–1 |
0,5 |
|
32 |
II |
1 |
2 |
8 |
9 |
3 |
–2 |
2 |
0,6 |
|
33 |
I |
1 |
3 |
10 |
6 |
4 |
1 |
3 |
0,7 |
|
34 |
II |
2 |
1 |
12 |
15 |
2 |
–3 |
1 |
0,8 |
|
35 |
I |
2 |
2 |
6 |
12 |
3 |
2 |
–2 |
0,9 |
|
36 |
II |
1 |
3 |
8 |
6 |
4 |
–1 |
3 |
1,0 |
|
|
в |
б |
а |
г |
в |
г |
в |
а |
г |
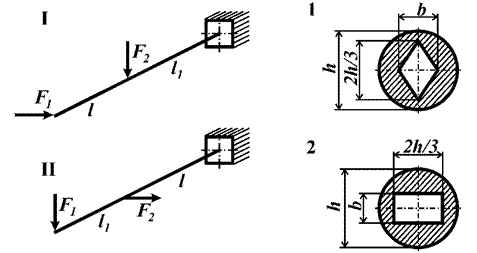
Рис.4
Задача 5. Расчет консольной балки,
подверженной косому изгибу. Определение допускаемой нагрузки.
Для балки (рис.5) найти допустимое значение параметра
нагрузки P.
Принять: l=1,5 м; материал Сталь 5; [n]=2; σт =280
мПа.
Остальные данные взять из табл.5 и рис.5.
Таблица 5
|
Номер cтроки |
Схема по рис.5 |
Тип сечения |
l1 /l |
l2 /l |
а, см |
F1/P |
F2/P |
F3/P |
F4/P |
|
01 |
I |
1 |
2 |
1 |
16 |
4 |
2 |
2 |
20 |
|
02 |
II |
2 |
1 |
2 |
10 |
1 |
4 |
3 |
10 |
|
03 |
I |
2 |
4 |
3 |
14 |
3 |
2 |
4 |
10 |
|
04 |
II |
1 |
3 |
4 |
12 |
2 |
2 |
5 |
5 |
|
05 |
I |
1 |
1 |
4 |
14 |
3 |
4 |
6 |
5 |
|
06 |
II |
2 |
3 |
3 |
10 |
1 |
2 |
4 |
10 |
|
07 |
I |
2 |
2 |
1 |
12 |
2 |
3 |
2 |
20 |
|
08 |
II |
1 |
4 |
2 |
16 |
4 |
1 |
3 |
15 |
|
09 |
I |
1 |
2 |
2 |
10 |
1 |
3 |
5 |
10 |
|
10 |
II |
2 |
3 |
3 |
12 |
2 |
2 |
6 |
10 |
|
11 |
I |
2 |
2 |
1 |
16 |
4 |
2 |
2 |
20 |
|
12 |
II |
1 |
1 |
2 |
10 |
1 |
4 |
3 |
10 |
|
13 |
I |
1 |
4 |
3 |
14 |
3 |
2 |
4 |
10 |
|
14 |
II |
2 |
3 |
4 |
12 |
2 |
2 |
5 |
5 |
|
15 |
I |
2 |
1 |
4 |
14 |
3 |
4 |
6 |
5 |
|
16 |
II |
1 |
3 |
3 |
10 |
1 |
2 |
4 |
10 |
|
17 |
I |
1 |
2 |
1 |
12 |
2 |
3 |
2 |
20 |
|
18 |
II |
2 |
4 |
2 |
16 |
4 |
1 |
3 |
15 |
|
19 |
I |
2 |
2 |
2 |
10 |
1 |
3 |
5 |
10 |
|
20 |
II |
1 |
3 |
3 |
12 |
2 |
2 |
6 |
10 |
|
21 |
I |
1 |
2 |
1 |
16 |
4 |
2 |
2 |
20 |
|
22 |
II |
2 |
1 |
2 |
10 |
1 |
4 |
3 |
10 |
|
23 |
I |
2 |
4 |
3 |
14 |
3 |
2 |
4 |
10 |
|
24 |
II |
1 |
3 |
4 |
12 |
2 |
2 |
5 |
5 |
|
25 |
I |
1 |
1 |
4 |
14 |
3 |
4 |
6 |
5 |
|
26 |
II |
2 |
3 |
3 |
10 |
1 |
2 |
4 |
10 |
|
27 |
I |
2 |
2 |
1 |
12 |
2 |
3 |
2 |
20 |
|
28 |
II |
1 |
4 |
2 |
16 |
4 |
1 |
3 |
15 |
|
29 |
I |
1 |
2 |
2 |
10 |
1 |
3 |
5 |
10 |
|
30 |
II |
2 |
3 |
3 |
12 |
2 |
2 |
6 |
10 |
|
31 |
I |
2 |
2 |
1 |
16 |
4 |
2 |
2 |
20 |
|
32 |
II |
1 |
1 |
2 |
10 |
1 |
4 |
3 |
10 |
|
33 |
I |
1 |
4 |
3 |
14 |
3 |
2 |
4 |
10 |
|
34 |
II |
2 |
3 |
4 |
12 |
2 |
2 |
5 |
5 |
|
35 |
I |
2 |
1 |
4 |
14 |
3 |
4 |
6 |
5 |
|
36 |
II |
1 |
3 |
3 |
10 |
1 |
2 |
4 |
10 |
|
|
в |
б |
а |
в |
г |
в |
а |
г |
б |
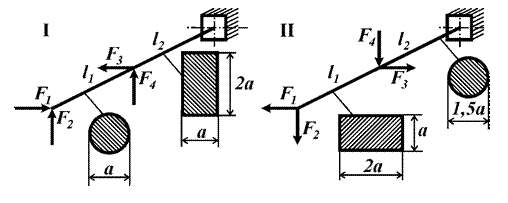
Рис.5
Задача 6. Расчет балки,
подверженной косому изгибу
Исходные
данные к задаче принимаются по табл. 6 и схемам на рис. 6.
1.
Нарисуйте в масштабе схему балки с нагрузками. Если нагрузка отрицательна,
покажите ее направленной в сторону, противоположную направлению, показанному на
рис. 6.
2.
Разложите нагрузки, если это необходимо, на направления главных осей инерции
балки. Постройте эпюры внутренних усилий.
3.
Найдите опасные сечения - сечения, в которых
действуют наиболее неблагоприятные сочетания изгибающих моментов.
4.
В одном из опасных сечений найдите положение опасных точек – точек с
максимальными нормальными напряжениями.
5.
Запишите условие прочности в опасных точках. Из условия прочности в точках,
расположенных в одном из опасных сечений, подберите размеры сечения балки. При
этом считайте, что балки прямоугольного сечения - деревянные, а балки из прокатного профиля - стальные. Для
найденных размеров сечения проверьте прочность в других опасных сечениях. Если
условие прочности не будет соблюдаться, подберите размеры сечения заново.
6.
Найдите полное перемещение точки оси балки, расположенной или на конце консоли,
или на сопряжении участков. Для этого сначала найдите вертикальную и
горизонтальную составляющие этого перемещения.
7.
Покажите на рисунке в масштабе поперечное сечение балки, нейтральную линию,
эпюру напряжений и полное перемещение. Найдите угол между нейтральной линией и
направлением полного перемещения.
8*. Сосчитайте экономию материала, которая произойдет,
если горизонтальная проекция нагрузки будет равна нулю, то есть балка будет
работать в условиях плоского изгиба.
Таблица 6
|
Номер строки |
l1, м |
q1, кН/м |
F1, кН |
Сечение |
l2, м |
q2, кН/м |
F2, кН |
M, кНм |
α, град |
Схема по рис.6 |
|
01 |
2 |
10 |
0 |
Двутавровое |
4 |
5 |
0 |
30 |
- |
1 |
|
02 |
2 |
0 |
40 |
2 швеллера [] |
2 |
0 |
-5 |
5 |
- |
2 |
|
03 |
1 |
-10 |
0 |
Прямоугольное, h/b
= 3 |
1 |
-5 |
0 |
-20 |
- |
3 |
|
04 |
2 |
0 |
-40 |
2 швеллера ][ |
1 |
0 |
5 |
-30 |
- |
4 |
|
05 |
2 |
20 |
0 |
Прямоугольное, h/b
= 3 |
1 |
4 |
0 |
-5 |
- |
5 |
|
06 |
1 |
0 |
50 |
Двутавровое |
2 |
0 |
10 |
-40 |
30 |
6 |
|
07 |
1 |
-20 |
0 |
Прямоугольное, h/b
= 2 |
2 |
-4 |
0 |
10 |
- |
7 |
|
08 |
2 |
0 |
-50 |
2 швеллера ][ |
4 |
0 |
-10 |
-10 |
- |
8 |
|
09 |
1 |
30 |
0 |
2 швеллера [] |
4 |
10 |
0 |
40 |
- |
9 |
|
10 |
2 |
0 |
30 |
Прямоугольное, h/b
= 2 |
2 |
0 |
20 |
20 |
- |
10 |
|
|
в |
г |
а |
б |
в |
г |
а |
б |
в |
г |
1 схема
2 схема
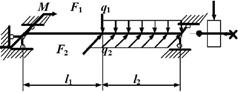
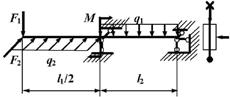
3 схема
4 схема
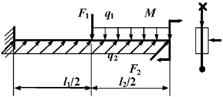
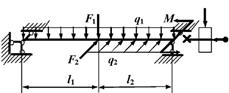
5 схема
6 схема
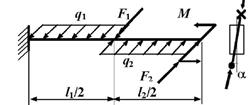
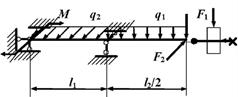
7 схема
8 схема
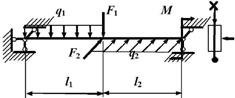
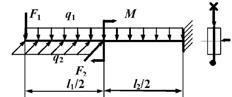
9 схема
10 схема
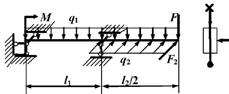
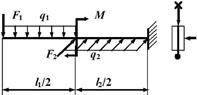
Рис.6
Задача 7. Расчет балки,
подверженной косому изгибу
Для
прямого стержня, нагруженного горизонтальными и вертикальными нагрузками по
схеме № 1 и 2 (рис.7 и 8, табл.7 и 8) и имеющего указанное сечение, требуется:
1. Определить
положение центра тяжести поперечного сечения (таблицы 9 и 10).
2. Вычислить
главные центральные моменты инерции поперечного сечения.
3. Вычертить
поперечное сечение в масштабе на отдельном листе с указанием основных осей и
необходимых размеров.
4. Записать
уравнения поперечных сил и изгибающих моментов в горизонтальной и вертикальной
плоскостях.
5. Построить
эпюры этих величин.
6. Выбрать
опасное сечение и найти в этом сечении изгибающие моменты относительно главных
осей инерции.
7. Найти
положение нулевой линии в опасном сечении.
8. Определить
положение опасных точек и замерить их координаты.
9. Вычислить
нормальные напряжения в этих точках.
10. Построить
эпюру нормальных напряжений в опасном сечении по нормали к нулевой линии.
11. Проверить
прочность стержня.
Исходные
данные к балке по схеме нагружения №1 на рис.7
принимаются по табл. 7.
Исходные
данные к балке по схеме нагружения №2 на рис.8
принимаются по табл. 8.
Исходные
данные к поперечным сечениям балок по схемам №1 и №2 принимаются по табл. 9 и 10.
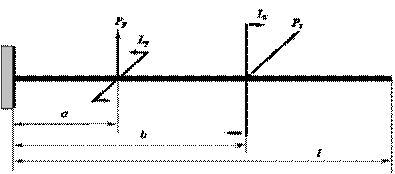
Рис. 7. Схема нагружения
№ 1
Таблица 7. Исходные данные к схеме нагружения
№1
|
Номер строки |
l, м |
а, м |
b, м |
Px, кН |
Py, кН |
Lx, кНм |
Ly, кНм |
[σ], МПа |
|
01 |
1,1 |
0,4 |
0,9 |
1 |
4,1 |
0,9 |
1 |
100 |
|
02 |
1 |
0,3 |
0,6 |
2 |
4,2 |
0,8 |
1 |
109 |
|
03 |
1,6 |
0,6 |
1,4 |
3 |
3,3 |
0,9 |
2 |
106 |
|
04 |
1,3 |
0,3 |
1,2 |
4 |
2,2 |
1,5 |
3 |
107 |
|
05 |
1,4 |
0,4 |
1,1 |
5 |
5,2 |
1,3 |
4 |
115 |
|
06 |
1 |
0,3 |
1 |
6 |
3,6 |
0,9 |
5 |
102 |
|
07 |
1,9 |
0,6 |
1,8 |
7 |
5 |
0,8 |
7 |
135 |
|
08 |
2 |
2 |
0,4 |
8 |
4,8 |
1,5 |
6 |
122 |
|
09 |
2 |
0,5 |
1,7 |
9 |
3,6 |
1,7 |
3 |
130 |
|
10 |
1,6 |
0,9 |
1,5 |
10 |
5,8 |
1,5 |
2,5 |
138 |
|
11 |
2,3 |
0,7 |
2,3 |
3,3 |
4,6 |
1,4 |
3,3 |
151 |
|
12 |
2,5 |
0,8 |
2,3 |
4,4 |
4,4 |
2,1 |
4,4 |
100 |
|
13 |
2,4 |
2,1 |
1,7 |
4,6 |
6,6 |
2 |
4,6 |
121 |
|
14 |
2,3 |
2,3 |
1,8 |
3,6 |
6 |
1 |
1,8 |
116 |
|
15 |
2,4 |
1,8 |
0,9 |
5,5 |
2,5 |
0,8 |
3,1 |
109 |
|
16 |
1,5 |
0,7 |
1,4 |
4,5 |
4,1 |
1,5 |
4,1 |
123 |
|
17 |
2,3 |
1,2 |
2 |
3,5 |
4,2 |
3,7 |
2,7 |
153 |
|
18 |
2,3 |
1,5 |
2,3 |
2,5 |
3,3 |
1,3 |
2,8 |
127 |
|
19 |
2,5 |
1,4 |
2,5 |
1,5 |
2,2 |
2 |
1,8 |
165 |
|
20 |
2 |
1,3 |
1,7 |
1,7 |
5,2 |
2 |
1,7 |
133 |
|
21 |
1,5 |
1 |
1,5 |
2,7 |
3,6 |
3,6 |
1,9 |
165 |
|
22 |
1,8 |
1,4 |
1,8 |
3,7 |
5 |
1,1 |
2,1 |
102 |
|
23 |
2 |
2 |
1,7 |
4,7 |
4,8 |
2,8 |
3,5 |
141 |
|
24 |
2,5 |
1,7 |
2,5 |
5,7 |
3,6 |
4,5 |
6,9 |
172 |
|
25 |
2 |
1,4 |
1,9 |
6,7 |
5,8 |
3,5 |
6,5 |
149 |
|
26 |
2 |
2 |
1,7 |
2,8 |
4,6 |
4 |
4,2 |
121 |
|
27 |
1,6 |
0,9 |
1,3 |
8,7 |
4,4 |
4,9 |
3,9 |
121 |
|
28 |
2 |
2 |
1,5 |
2,4 |
6,6 |
1,3 |
2 |
172 |
|
29 |
1,4 |
0,8 |
1,1 |
1,9 |
6 |
5 |
2,3 |
182 |
|
30 |
2,3 |
1,5 |
2,2 |
1,1 |
2,5 |
4,5 |
2,9 |
137 |
|
|
г |
в |
б |
а |
г |
в |
б |
а |
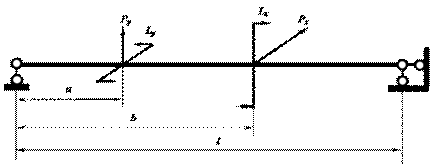
Рис.8. Схема нагружения
№ 2
Таблица 8. Исходные данные к схеме нагружения
№2
|
Номер строки |
l, м |
а, м |
b, м |
Px, кН |
Py, кН |
Lx, кНм |
Ly, кНм |
[σ], МПа |
|
01 |
1,3 |
0,4 |
0,7 |
3 |
4,3 |
0,8 |
1,2 |
108 |
|
02 |
1 |
0,2 |
0,6 |
1 |
2,8 |
1,5 |
1,3 |
103 |
|
03 |
1,2 |
0,4 |
0,6 |
1,2 |
3,1 |
2,2 |
2,5 |
110 |
|
04 |
1,3 |
0,9 |
0,4 |
1,3 |
2,6 |
1,3 |
2,3 |
126 |
|
05 |
1,4 |
0,6 |
1 |
1 |
2,5 |
2,6 |
2,3 |
117 |
|
06 |
1,8 |
1,2 |
0,3 |
1,3 |
2,2 |
1,4 |
2,5 |
129 |
|
07 |
1,3 |
0,5 |
0,9 |
1,3 |
3,2 |
0,9 |
2,5 |
105 |
|
08 |
1,2 |
0,8 |
0,5 |
2,1 |
2,2 |
1,2 |
1,9 |
107 |
|
09 |
1,2 |
0,7 |
1 |
2 |
2,9 |
3,1 |
2 |
121 |
|
10 |
2,2 |
1,7 |
0,4 |
2,5 |
3 |
1,9 |
3 |
114 |
|
11 |
2,1 |
0,9 |
1,7 |
3,1 |
4,7 |
1,5 |
3,2 |
138 |
|
12 |
2,3 |
1,9 |
0,7 |
3,4 |
4,6 |
2,9 |
2,7 |
118 |
|
13 |
1,7 |
1,5 |
0,9 |
1,3 |
5,2 |
2,2 |
3,4 |
111 |
|
14 |
1,9 |
0,6 |
1,6 |
1,9 |
2,7 |
3,2 |
2,5 |
154 |
|
15 |
1,6 |
0,8 |
1,3 |
3,9 |
5,7 |
2,6 |
3,8 |
121 |
|
16 |
1,3 |
1,3 |
0,2 |
1,8 |
5,3 |
3,1 |
3,1 |
167 |
|
17 |
2,4 |
1,9 |
0,7 |
2,3 |
4,1 |
2,2 |
1,9 |
160 |
|
18 |
2,3 |
0,7 |
1,7 |
1,5 |
5,4 |
1,3 |
4,1 |
135 |
|
19 |
1,4 |
0,7 |
1 |
1,3 |
2,8 |
3,7 |
3,5 |
130 |
|
20 |
2,4 |
0,9 |
2 |
1,2 |
5,2 |
0,8 |
2,6 |
160 |
|
21 |
2,3 |
1,6 |
0,7 |
1 |
2,3 |
2,5 |
1,3 |
128 |
|
22 |
1,5 |
0,8 |
1,2 |
1,9 |
2 |
5,3 |
3,9 |
117 |
|
23 |
1 |
0,3 |
0,8 |
1,4 |
5,7 |
3,5 |
3,9 |
168 |
|
24 |
1 |
0,2 |
0,7 |
4,1 |
4,8 |
2,9 |
4,1 |
112 |
|
25 |
1,2 |
0,7 |
1 |
5,2 |
2,5 |
4,2 |
4,6 |
104 |
|
26 |
1,1 |
0,6 |
0,4 |
2 |
2,3 |
2,3 |
4,2 |
120 |
|
27 |
2,2 |
1,7 |
0,4 |
4,8 |
2,6 |
2 |
3,4 |
147 |
|
28 |
1 |
0,4 |
0,6 |
2,2 |
5,2 |
1,3 |
1,9 |
105 |
|
29 |
2,3 |
1,6 |
0,3 |
2,3 |
4,3 |
5,1 |
5,1 |
166 |
|
30 |
2,1 |
0,4 |
1,9 |
3,7 |
5,9 |
6,2 |
3,6 |
185 |
|
|
а |
б |
в |
г |
а |
б |
в |
г |
Таблица 9. Поперечные сечения балок к схемам нагружения
№1 и №2
|
Схема 1
|
Схема 2
|
Схема 3
|
|
Схема 4
|
Схема 5
|
Схема 6
|
|
Схема 7
|
Схема 8
|
Схема 9
|
|
Схема 10
|
Схема 11
|
Схема 12
|
|
Схема 13
|
Схема 14
|
Схема 15
|
|
Схема 16
|
Схема 17
|
Схема 18
|
|
Схема 19
|
Схема 20
|
Схема 21
|
|
Схема 22
|
Схема 23
|
Схема 24
|
|
Схема 25
|
Схема 26
|
Схема 27
|
|
Схема 28
|
Схема 29
|
Схема 30
|
Таблица 10.
Исходные данные к поперечным сечениям по таблице 9
|
Номер строки |
Сечение угловое
неравнополочное
|
Сечение швеллерное |
Сечение двутавровое |
a, мм |
b, мм |
|
|
01 |
8/5 |
7,5 |
12 |
12 |
196 |
26 |
|
02 |
8/5 |
7 |
10 |
10 |
60 |
12 |
|
03 |
7/4,5 |
8 с |
14 |
16 |
179 |
27 |
|
04 |
5/3,2 |
5 |
8 |
10 |
86 |
19 |
|
05 |
6,3/4 |
6,3 |
16 |
14 |
127 |
39 |
|
06 |
7,5/5 с |
5,6 в |
16 |
16 |
176 |
18 |
|
07 |
9/5,6 |
7,5 с |
18 |
16 |
136 |
33 |
|
08 |
7/4,5 |
8 |
16 |
14 |
180 |
21 |
|
09 |
9/5,6 в |
8 |
10 |
12 |
125 |
40 |
|
10 |
7/5 |
7,5 в |
18 |
16 |
82 |
34 |
|
11 |
6,3/4 |
5,6 в |
8 |
10 |
189 |
32 |
|
12 |
7,5/5 |
7 |
10 |
14 |
174 |
19 |
|
13 |
8/5 |
6,3 |
16 |
14 |
141 |
38 |
|
14 |
7/4,5 |
8 с |
10 |
16 |
72 |
11 |
|
15 |
7,5/5 с |
7 с |
16 |
16 |
137 |
14 |
|
16 |
8/5 |
9 в |
16 |
14 |
186 |
39 |
|
17 |
6,3/4 |
5 с |
12 |
14 |
149 |
37 |
|
18 |
7,5/5 |
7 с |
14 а |
16 |
96 |
39 |
|
19 |
5,6/3,6 |
6,3 |
12 |
14 |
105 |
19 |
|
20 |
8/5 |
7 с |
16 |
14 |
110 |
20 |
|
21 |
7/4,5 |
6,3 в |
10 |
12 |
90 |
12 |
|
22 |
6,3/4 с |
7 в |
14 а |
16 |
192 |
17 |
|
23 |
6,3/4 |
8 |
12 |
14 |
130 |
12 |
|
24 |
5,6/3,6 |
5,6 в |
14 |
12 |
179 |
37 |
|
25 |
9/5,6 |
7 |
16 |
14 |
145 |
15 |
|
26 |
7/4,5 |
8 с |
14 в |
16 |
116 |
14 |
|
27 |
5/3,2 |
7,5 с |
16 |
16 |
145 |
37 |
|
28 |
8/5 |
8 в |
12 |
16 |
172 |
11 |
|
29 |
6,3/4 |
7 |
16 |
10 |
183 |
13 |
|
30 |
7/4,5 |
9 |
12 |
12 |
121 |
17 |
|
|
г |
б |
а |
в |
г |
а |
Задача 8. Расчет балки,
подверженной растяжению с изгибом
Для
прямого стержня, нагруженного по схеме № 1 и 2 (рис. 9 и 10, табл.11 и 12) и имеющего
указанное поперечное сечение (таблица 13), требуется:
1. Определить
положение центра тяжести поперечного сечения.
2. Вычислить
главные центральные моменты инерции поперечного сечения.
3. Привести
все силы к оси стержня.
4. Записать
выражения продольной силы N(z), поперечной силы Qy(z) и изгибающего момента Mx(z).
5. Построить
эпюры этих функций.
6. Выбрать
опасное сечение.
7. Записать
уравнение и построить нулевую линию в опасном сечении.
8. Вычислить
напряжение в опасных точках этого сечения.
9. Построить
эпюру нормальных напряжений в опасном сечении.
10. Проверить
прочность стержня.
Исходные
данные к балке по схеме нагружения №1 на рис.9
принимаются по табл. 11.
Исходные
данные к балке по схеме нагружения №2 на рис.10
принимаются по табл. 12.
Исходные
данные к поперечным сечениям балок по схемам №1 и №2 принимаются по табл. 13.
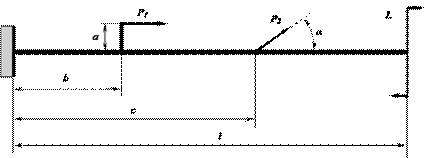
Рис. 9. Схема нагружения
№ 1
Таблица 11. Исходные данные к схеме нагружения №1
|
Номер строки |
l,
м |
a,
м |
b,
м
|
c,
м
|
r,
м |
P1, кН |
P2, кН |
L, кНм |
α |
[σ], МПа |
|
01 |
1,7 |
0,2 |
0,5 |
1,2 |
15 |
5 |
7,5 |
0,5 |
11° |
102 |
|
02 |
1,4 |
0,1 |
0,4 |
1 |
12 |
4 |
9 |
0,1 |
-17° |
100 |
|
03 |
1,7 |
0,3 |
0,4 |
1,3 |
11 |
4 |
4 |
1,2 |
-15° |
120 |
|
04 |
1,3 |
0,2 |
0,3 |
0,8 |
14 |
-3 |
3 |
0,6 |
19° |
115 |
|
05 |
2,2 |
0,3 |
0,7 |
1,6 |
40 |
2,5 |
-5 |
0,2 |
21° |
118 |
|
06 |
1,9 |
0,2 |
0,6 |
1,7 |
13 |
-3 |
-4,5 |
0,6 |
19° |
146 |
|
07 |
2,5 |
0,3 |
1 |
2 |
23 |
3,2 |
8 |
1 |
-19° |
158 |
|
08 |
1,7 |
0,2 |
0,4 |
1,3 |
24 |
-3,5 |
-6 |
0,2 |
18° |
153 |
|
09 |
2 |
0,3 |
1,8 |
0,9 |
9 |
3,5 |
7 |
1,1 |
-32° |
101 |
|
10 |
2 |
0,2 |
0,5 |
1,6 |
22 |
7 |
7 |
-1,4 |
20° |
163 |
|
11 |
1,8 |
0,3 |
0,5 |
1 |
11 |
-5 |
-5 |
1,5 |
17° |
158 |
|
12 |
2,4 |
0,3 |
1,7 |
0,7 |
25 |
8,8 |
11 |
2,6 |
35° |
162 |
|
13 |
2,5 |
0,1 |
2,3 |
1,4 |
16 |
-7 |
-4,6 |
1,2 |
36° |
109 |
|
14 |
2,5 |
0,1 |
0,6 |
1,9 |
18 |
5,2 |
13 |
0,5 |
-34° |
152 |
|
15 |
2,4 |
0,3 |
0,7 |
1,8 |
17 |
-2,4 |
-6 |
0,7 |
40° |
155 |
|
16 |
1,6 |
0,2 |
1,1 |
0,6 |
29 |
-7 |
-14 |
1,4 |
37° |
116 |
|
17 |
2,3 |
0,2 |
0,4 |
1,7 |
22 |
5 |
10 |
0,5 |
-39° |
143 |
|
18 |
2,4 |
0,1 |
0,5 |
1,9 |
17 |
-11 |
11 |
1,1 |
-41° |
134 |
|
19 |
1,1 |
0,3 |
0,9 |
0,4 |
16 |
-15 |
-15 |
3 |
26° |
159 |
|
20 |
2,5 |
0,3 |
0,4 |
1,9 |
19 |
7,2 |
9 |
2,2 |
27° |
169 |
|
21 |
1,9 |
0,1 |
0,4 |
1,7 |
24 |
-7,6 |
4,6 |
1,5 |
24° |
134 |
|
22 |
1,6 |
0,3 |
1,3 |
0,4 |
10 |
6,4 |
16 |
1,9 |
-29° |
100 |
|
23 |
1,5 |
0,3 |
0,4 |
1,2 |
25 |
-1,6 |
-4 |
0,5 |
13° |
149 |
|
24 |
1,4 |
0,2 |
0,8 |
0,4 |
27 |
6,5 |
12 |
1,8 |
-21° |
127 |
|
25 |
2,5 |
0,3 |
0,6 |
1,9 |
16 |
8,5 |
- 6 |
2,5 |
-11° |
140 |
|
26 |
1,2 |
0,2 |
1 |
0,5 |
20 |
8 |
- 7,5 |
1,8 |
17° |
138 |
|
27 |
2,5 |
0,3 |
0,6 |
2,1 |
15 |
16 |
20 |
2,3 |
12° |
111 |
|
28 |
1,2 |
0,2 |
0,3 |
1 |
13 |
- 4,8 |
-6 |
1 |
17° |
156 |
|
29 |
2,2 |
0,1 |
0,5 |
1,9 |
27 |
6 |
- 2 |
0,2 |
-43° |
184 |
|
30 |
2,3 |
0,3 |
0,5 |
1,7 |
26 |
- 9,2 |
- 6,5 |
2,8 |
43° |
147 |
|
|
в |
г |
б |
а |
в |
г |
б |
а |
в |
г |
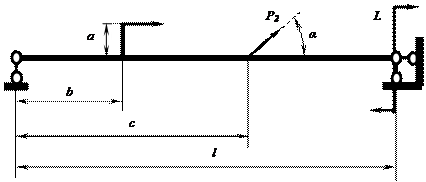
Рис.10. Схема нагружения
№ 2
Таблица 12. Исходные данные к схеме нагружения №2
|
Номер строки |
l,
м |
a,
м |
b,
м
|
c,
м
|
r,
м |
P1, кН |
P2, кН |
L, кНм |
α |
[σ], МПа |
|
01 |
1 |
0,2 |
0,8 |
0,3 |
11 |
-5 |
-3,6 |
0,1 |
10° |
103 |
|
02 |
1,1 |
0,1 |
0,2 |
0,7 |
12 |
7 |
4 |
0,1 |
-12° |
109 |
|
03 |
1,1 |
0,3 |
0,8 |
0,2 |
21 |
4,5 |
3 |
0,3 |
-21° |
102 |
|
04 |
1,5 |
0,2 |
0,3 |
1,3 |
24 |
-5 |
-3,5 |
0,4 |
13° |
100 |
|
05 |
1,2 |
0,2 |
0,4 |
0,9 |
23 |
4 |
5,5 |
0,3 |
24° |
124 |
|
06 |
1,1 |
0,2 |
0,3 |
0,8 |
40 |
-5,6 |
-7 |
1,1 |
15° |
118 |
|
07 |
1 |
0,1 |
0,3 |
0,8 |
13 |
4,5 |
3 |
0,3 |
-23° |
132 |
|
08 |
2,2 |
0,2 |
0,4 |
1,8 |
31 |
-2,8 |
-7 |
0,6 |
27° |
111 |
|
09 |
2,2 |
0,3 |
0,4 |
1,7 |
17 |
5 |
-4,5 |
0,6 |
-30° |
106 |
|
10 |
2,4 |
0,3 |
0,5 |
2 |
14 |
4 |
4 |
1,2 |
-20° |
133 |
|
11 |
1,2 |
0,2 |
1 |
0,2 |
22 |
-6 |
-6 |
1,2 |
20° |
152 |
|
12 |
2 |
0,3 |
0,4 |
1,6 |
27 |
9,6 |
12 |
2,9 |
35° |
129 |
|
13 |
1,7 |
0,3 |
0,3 |
1,5 |
37 |
-8 |
-10 |
2,4 |
34° |
101 |
|
14 |
2,1 |
0,3 |
0,5 |
2 |
28 |
2,5 |
6,5 |
0,5 |
-12° |
134 |
|
15 |
2,5 |
0,1 |
0,3 |
1,8 |
10 |
-12 |
-13 |
0,5 |
36° |
146 |
|
16 |
2,2 |
0,2 |
0,6 |
1,9 |
18 |
-6,5 |
-13 |
1,3 |
40° |
159 |
|
17 |
1,8 |
0,3 |
1,5 |
0,3 |
34 |
4,5 |
9 |
1,4 |
-30° |
129 |
|
18 |
2,5 |
0,3 |
0,4 |
2 |
29 |
6 |
4 |
0,3 |
-38° |
103 |
|
19 |
2,4 |
0,3 |
0,4 |
1,9 |
25 |
-20 |
-20 |
6 |
42° |
131 |
|
20 |
1,3 |
0,3 |
0,4 |
1 |
20 |
16 |
20 |
4,8 |
35° |
156 |
|
21 |
1,2 |
0,2 |
0,4 |
0,7 |
39 |
-15 |
-24 |
3,8 |
22° |
125 |
|
22 |
1 |
0,1 |
0,2 |
0,8 |
30 |
5,6 |
14 |
0,6 |
-13° |
154 |
|
23 |
2 |
0,3 |
0,7 |
1,7 |
10 |
-7,6 |
-19 |
2,3 |
23° |
171 |
|
24 |
1,7 |
0,3 |
0,4 |
1,1 |
34 |
5 |
19 |
2,9 |
-34° |
142 |
|
25 |
2,1 |
0,2 |
0,6 |
1,8 |
33 |
4 |
4 |
0,8 |
-28° |
155 |
|
26 |
1,7 |
0,3 |
1,3 |
0,3 |
38 |
-5 |
-5 |
1,5 |
38° |
109 |
|
27 |
2 |
0,1 |
0,4 |
1,4 |
42 |
8 |
10 |
0,1 |
17° |
141 |
|
28 |
1,4 |
0,3 |
0,2 |
1 |
49 |
-12 |
-15 |
2,5 |
22° |
169 |
|
29 |
1,7 |
0,3 |
0,6 |
1,2 |
43 |
8,4 |
21 |
2,5 |
-40° |
181 |
|
30 |
1,3 |
0,2 |
0,3 |
0,8 |
50 |
-11 |
-16 |
2,2 |
15° |
115 |
|
|
в |
г |
а |
б |
в |
г |
а |
б |
в |
г |
Таблица 13. Поперечные сечения балок к схемам нагружения
№1 и №2
|
Схема 1
|
Схема 2
|
Схема 3
|
|
Схема 4
|
Схема 5
|
Схема 6
|
|
Схема 7
|
Схема 8
|
Схема 9
|
|
Схема 10
|
Схема 11
|
Схема 12
|
|
Схема 13
|
Схема 14
|
Схема 15
|
|
Схема 16
|
Схема 17
|
Схема 18
|
|
Схема 19
|
Схема 20
|
Схема 21
|
|
Схема 22
|
Схема 23
|
Схема 24
|
|
Схема 25
|
Схема 26
|
Схема 27
|
|
Схема 28
|
Схема 29
|
Схема 30
|
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов