Главная
Кинематический и силовой расчеты
рычажного шестизвенника
Задание.
1. Число оборотов кривошипа n1=60 об/мин. Угловая скорость кривошипа ![]() является постоянной.
является постоянной.
2. Размеры звеньев: О1А=0,15 м, АВ=0,2
м, ВС=0,5 м, ВО2=0,185 м. Центры масс
звеньев расположены по середине соответствующих звеньев.
3. Массы звеньев: m1=1,5 кг, m2=2 кг, m3 =
4. Момент инерции относительно оси, проходящей через
центр масс звена: IS2=0,05, IS3=0,06, IS4=0,05.
5. Рабочие усилие: F=40 Н.
1.
Структурный анализ механизма
1.1.
Структурная схема механизма
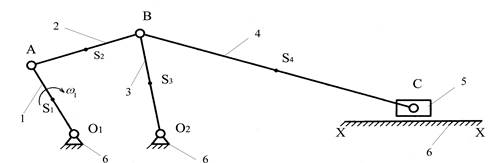
1.2. Звенья механизма
|
Звено |
Наименование |
Подвижность |
Число подвижных
звеньев |
|
1 |
Кривошип |
Подвижное |
n=5 |
|
2 |
Шатун |
Подвижное |
|
|
3 |
Коромысло |
Подвижное |
|
|
4 |
Шатун |
Подвижное |
|
|
5 |
Ползун |
Подвижное |
|
|
6 |
Стойка |
Неподвижное |
1.3. Кинематические
пары
|
№ п/п |
Обозначение на структурной схеме |
Соединяемые звенья |
Вид |
Тип кинематической
пары |
Индекс |
|
|
Характер соприкосновения |
Степень подвижности |
|||||
|
1 |
О1 |
1,6 |
Вращат. |
Низшая |
Одноподвижная |
|
|
2 |
А |
1,2 |
Вращат. |
Низшая |
Одноподвижная |
ВA(1,2) |
|
3 |
В |
2,3 |
Вращат. |
Низшая |
Одноподвижная |
ВB(2,3) |
|
4 |
В |
3,4 |
Вращат. |
Низшая |
Одноподвижная |
ВВ(3,4) |
|
5 |
С |
4,5 |
Вращат. |
Низшая |
Одноподвижная |
ВC(4,5) |
|
6 |
С |
5,6 |
Поступат. |
Низшая |
Одноподвижная |
ПС(5,6) |
|
7 |
О2 |
3,6 |
Вращат. |
Низшая |
Одноподвижная |
|
Число одноподвижных
кинематических пар p1=7, число двух подвижных кинематических
пар р2=0.
1.4. Степень подвижности механизма
![]() .
.
1.5. Строение групп Ассура
1.5.1. Последняя группа Ассура
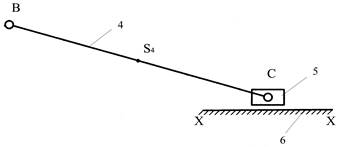
II класс, 2 порядок, вид
ВВП.
Степень подвижности: ![]() .
.
Структурная формула:
![]()
1.5.2.
Предпоследняя группа Асcура
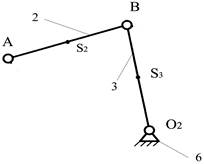
II класс, 2 порядок,
вид ВВВ
Степень подвижности ![]() .
.
Структурная формула:
![]()
1.5.3.
Начальный механизм
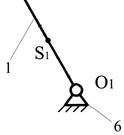
I класс
Степень подвижности ![]() .
.
Структурная формула:
![]()
1.6. Структурная формула всего механизма
![]()
1.7. Класс всего механизма II, так как
наивысший класс группы Ассура, входящей в данный механизм II.
2. Кинематический
анализ механизма
2.1. Определение
скоростей точек звеньев и угловых скоростей звеньев
Построим кинематическую схему механизма в
масштабе ![]() =0,05 м/мм.
=0,05 м/мм.
2.1.1. Определение
угловой скорости кривошипа:
![]()
2.1.2. Определение
скорости точки А:
![]() м/с.
м/с.
Вектор скорости ![]() перпендикулярен
кривошипу О1А.
перпендикулярен
кривошипу О1А.
Выбираем масштаб плана скоростей ![]() .
.
Найдём отрезок, изображающий вектор скорости ![]() на плане:
на плане:
![]() .
.
Из полюса плана скоростей ![]() откладываем данный отрезок перпендикулярно О1А в направлении угловой
скорости
откладываем данный отрезок перпендикулярно О1А в направлении угловой
скорости ![]() .
.
2.1.3.
Определение скорости точки В:
Запишем векторное уравнение:
![]() .
.
Направления векторов скоростей: ![]() .
.
Продолжим строить план скоростей.
Из конца вектора ![]() (точка а) проводим направление вектора
(точка а) проводим направление вектора ![]() . Из полюса (точка
. Из полюса (точка ![]() ) проводим направление вектора
) проводим направление вектора ![]() . На пересечении двух проведённых направлений получим
точку b. Измеряя длины полученных отрезков и умножая их на
масштаб
. На пересечении двух проведённых направлений получим
точку b. Измеряя длины полученных отрезков и умножая их на
масштаб ![]() , получим значения скоростей:
, получим значения скоростей:
![]() м/с;
м/с;
![]() м/с.
м/с.
2.1.4.
Определение скорости точки С:
Запишем векторное уравнение:
![]() .
.
Направления векторов скоростей: ![]() .
.
Продолжим строить план скоростей.
Из конца вектора ![]() (точка b) проводим
направление вектора
(точка b) проводим
направление вектора![]() . Из полюса (точка
. Из полюса (точка ![]() ) проводим направление вектора
) проводим направление вектора ![]() . На пересечении двух проведённых направлений получим
точку c. Измеряя длины полученных отрезков и умножая их на
масштаб
. На пересечении двух проведённых направлений получим
точку c. Измеряя длины полученных отрезков и умножая их на
масштаб ![]() , получим значения скоростей:
, получим значения скоростей:
![]() м/с;
м/с;
![]() м/с.
м/с.
2.1.5.
Определение угловой скорости шатуна АВ:
![]() .
.
Для определения направления ω2
переносим вектор ![]() в точку В шатуна АВ и смотрим как она движется
относительно точки А. Направление
этого движения соответствует
в точку В шатуна АВ и смотрим как она движется
относительно точки А. Направление
этого движения соответствует ![]() . В данном случае угловая скорость
. В данном случае угловая скорость ![]() направлена по
часовой стрелке.
направлена по
часовой стрелке.
2.1.6.
Определение угловой скорости коромысла ВО2:
![]() .
.
Для определения направления ω3 переносим вектор ![]() в точку В коромысла ВО2 и смотрим как она движется
относительно точки О2.
Направление этого движения соответствует
в точку В коромысла ВО2 и смотрим как она движется
относительно точки О2.
Направление этого движения соответствует ![]() . В данном случае угловая скорость
. В данном случае угловая скорость ![]() направлена по
часовой стрелке.
направлена по
часовой стрелке.
2.1.7.
Определение угловой скорости шатуна ВС:
![]() .
.
Для определения направления ω4 переносим вектор ![]() в точку С шатуна CB и смотрим,
как она движется относительно точки В.
Направление этого движения соответствует
в точку С шатуна CB и смотрим,
как она движется относительно точки В.
Направление этого движения соответствует ![]() . В данном случае угловая скорость
. В данном случае угловая скорость ![]() направлена по
часовой стрелке.
направлена по
часовой стрелке.
|
Исследуемая величина |
Отрезок на плане |
Направление |
Величина отрезка на плане, мм |
Масштабный коэффициент, |
Значение величины, м/с |
|
|
|
|
94 |
|
0,94 |
|
|
|
|
92 |
0,92 |
|
|
|
ab |
|
31 |
0,31 |
|
|
|
|
|
86 |
0,86 |
|
|
|
cb |
|
17 |
0,17 |
|
|
|
По часовой стрелке |
1,55 с–1 |
|||
|
|
По часовой стрелке |
4,97 с–1 |
|||
|
|
Против часовой стрелки |
0,34 с–1 |
|||
Кинематическая схема
механизма ![]()
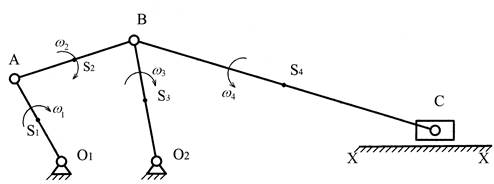
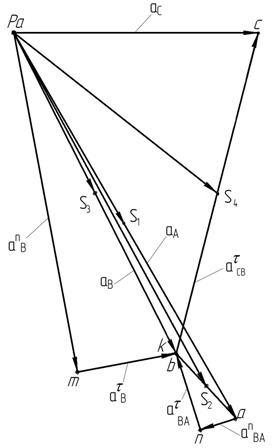
План
скоростей ![]()
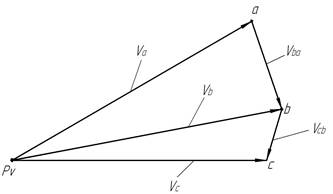
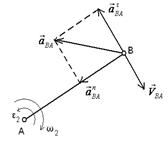
2.2. Определение
ускорений точек звеньев и угловых ускорений звеньев
2.2.1.Определение
ускорения точки А:
Так как угловая скорость ![]() является
постоянной, то
является
постоянной, то ![]() .
.
![]() . Вектор ускорения
. Вектор ускорения ![]() направлен
параллельно кривошипу О1А
от точки А к
точке О1.
направлен
параллельно кривошипу О1А
от точки А к
точке О1.
Выбираем масштаб плана ускорений ![]() . Найдём отрезок, изображающий вектор ускорения
. Найдём отрезок, изображающий вектор ускорения ![]() на плане:
на плане: ![]() мм. Из полюса
плана ускорений
мм. Из полюса
плана ускорений ![]() откладываем
данный отрезок в направлении, параллельном АО1.
откладываем
данный отрезок в направлении, параллельном АО1.
2.2.2.
Определение ускорения точки В:
Запишем векторное уравнение: ![]() .
.
Вектор относительного ускорения ![]() раскладываем на
нормальную и касательную составляющие:
раскладываем на
нормальную и касательную составляющие: ![]() .
.
Нормальное относительное ускорение
равно: ![]() м/с2.
м/с2.
Найдём отрезок, изображающий вектор
ускорения ![]() на плане:
на плане:
![]() мм.
мм.
Продолжаем строить план ускорений.
Вектор ускорения ![]() направлен параллельно
АВ. Откладываем отрезок an из точки a плана
ускорений в указанном направлении от точки В к точке А.
направлен параллельно
АВ. Откладываем отрезок an из точки a плана
ускорений в указанном направлении от точки В к точке А.
Вектор ускорения ![]() направлен
перпендикулярно АВ. Проводим это
направление из точки n плана ускорений.
направлен
перпендикулярно АВ. Проводим это
направление из точки n плана ускорений.
Вектор ускорения ![]() раскладываем на
нормальную и касательную составляющие:
раскладываем на
нормальную и касательную составляющие:
![]() .
.
Нормальное ускорение равно: ![]() м/с2.
м/с2.
Найдём отрезок, изображающий вектор
ускорения ![]() на плане:
на плане: ![]() мм.
мм.
Продолжаем строить план ускорений.
Вектор ускорения ![]() направлен
параллельно ВO2.
Откладываем отрезок
направлен
параллельно ВO2.
Откладываем отрезок ![]() из точки
из точки ![]() плана ускорений
в указанном направлении от точки В к точке O2. Вектор ускорения
плана ускорений
в указанном направлении от точки В к точке O2. Вектор ускорения ![]() направлен
перпендикулярно ВO2.
Проводим это направление из точки m плана
ускорений. Две прямые линии, проведённые
из точек n и m в
указанных направлениях, пересекаются в точке b.
направлен
перпендикулярно ВO2.
Проводим это направление из точки m плана
ускорений. Две прямые линии, проведённые
из точек n и m в
указанных направлениях, пересекаются в точке b.
Найдем величины ускорений. Измеряя
длины полученных отрезков и умножая их на масштаб![]() , получим:
, получим:
![]() м/с2;
м/с2;
![]() м/с2;
м/с2;
![]() м/с2;
м/с2;
![]() м/с2.
м/с2.
2.2.3.
Определение ускорения точки C:
Запишем векторное уравнение: ![]() .
.
Вектор относительного ускорения ![]() раскладываем на
нормальную и касательную составляющие:
раскладываем на
нормальную и касательную составляющие: ![]() .
.
Нормальное относительное ускорение
равно:
![]() м/с2.
м/с2.
Найдём отрезок, изображающий вектор ускорения ![]() на плане:
на плане: ![]() мм. Продолжаем
строить план ускорений. Так как отрезок bk мал, то его на плане ускорений не откладываем. Точки b и k совпадают.
мм. Продолжаем
строить план ускорений. Так как отрезок bk мал, то его на плане ускорений не откладываем. Точки b и k совпадают.
Вектор ускорения ![]() направлен
перпендикулярно ВС. Проводим это
направление из точки k плана ускорений.
направлен
перпендикулярно ВС. Проводим это
направление из точки k плана ускорений.
Вектор ускорения ![]() направлен
параллельно оси X–X. Проводим это направление из полюса
направлен
параллельно оси X–X. Проводим это направление из полюса ![]() . Две прямые линии, проведённые из точек k и
. Две прямые линии, проведённые из точек k и ![]() в указанных
направлениях, пересекаются в точке c.
в указанных
направлениях, пересекаются в точке c.
Найдем величины ускорений. Измеряя
длины полученных отрезков и умножая их на масштаб![]() , получим:
, получим:
![]() м/с2;
м/с2;
![]() м/с2;
м/с2;
![]() м/с2.
м/с2.
2.2.4.
Определение ускорения точки S1:
![]() м/с2. Вектор ускорения
м/с2. Вектор ускорения ![]() направлен
параллельно кривошипу О1А
от точки S1 к точке О1.
направлен
параллельно кривошипу О1А
от точки S1 к точке О1.
2.2.5.
Определение ускорения точки S2:
Воспользуемся следствием из теоремы
подобия. Составим пропорцию:
![]()
Данный отрезок откладываем на прямой ab от точки a. Точку s2 соединяем с полюсом
pa.
Величина ускорения: ![]() м/с2.
м/с2.
2.2.6.
Определение ускорения точки S3:
Воспользуемся следствием из теоремы
подобия. Составим пропорцию:
![]()
Данный отрезок откладываем на прямой pab от
точки b. Точку s3 соединяем с полюсом pa.
Величина ускорения: ![]() м/с2.
м/с2.
2.2.7.
Определение ускорения точки S4:
Воспользуемся следствием из теоремы
подобия. Составим пропорцию:
![]()
Данный отрезок откладываем на прямой bc от точки b. Точку ![]() соединяем с
полюсом pa.
соединяем с
полюсом pa.
Величина ускорения: ![]() м/с2.
м/с2.
2.2.8.
Определение углового ускорения шатуна АВ:
![]()
Для определения направления ![]() переносим
вектор
переносим
вектор ![]() в точку В шатуна АВ и смотрим, как она движется
относительно точки А. Направление
этого движения соответствует
в точку В шатуна АВ и смотрим, как она движется
относительно точки А. Направление
этого движения соответствует![]() . В данном случае угловое ускорение
. В данном случае угловое ускорение ![]() направлено
против часовой стрелки.
направлено
против часовой стрелки.
2.2.9.
Определение углового ускорения коромысла ВO2:
![]()
Для определения направления ![]() переносим
вектор
переносим
вектор ![]() в точку В коромысла ВО2 и смотрим, как она
движется относительно точки О2.
Направление этого движения соответствует
в точку В коромысла ВО2 и смотрим, как она
движется относительно точки О2.
Направление этого движения соответствует![]() . В данном случае угловое ускорение
. В данном случае угловое ускорение ![]() направлено по
часовой стрелке.
направлено по
часовой стрелке.
2.2.10.
Определение углового ускорения шатуна ВС:
![]()
Для определения направления ![]() переносим
вектор
переносим
вектор ![]() в точку C шатуна ВС и смотрим, как она движется
относительно точки B. Направление этого движения соответствует. В данном
случае угловое ускорение
в точку C шатуна ВС и смотрим, как она движется
относительно точки B. Направление этого движения соответствует. В данном
случае угловое ускорение ![]() направлено
против часовой стрелки.
направлено
против часовой стрелки.
|
Исследуемая величина |
Отрезок на плане |
Направление |
Величина отрезка на плане, мм |
Масштабный коэффициент
|
Значение величины, м/с2 |
|
|
|
|
118 |
|
5,9 |
|
|
|
|
10 |
0,48 |
|
|
|
|
|
21 |
1,05 |
|
|
|
|
|
23 |
1,15 |
|
|
|
|
|
91 |
4,57 |
|
|
|
|
|
27 |
1,35 |
|
|
|
|
|
95 |
4,75 |
|
|
|
|
|
1 |
0,058 |
|
|
|
|
|
88 |
4,4 |
|
|
|
|
|
88 |
4,4 |
|
|
|
|
|
65 |
3,25 |
|
|
|
|
|
59 |
2,95 |
|
|
|
|
|
107 |
5,35 |
|
|
|
|
|
48 |
2,4 |
|
|
|
|
|
69 |
3,45 |
|
|
|
Против часовой стрелки |
5,25 с–2 |
|||
|
|
По часовой стрелке |
25,68 с–2 |
|||
|
|
Против часовой стрелки |
2,2 с–2 |
|||
Кинематическая схема
механизма ![]()
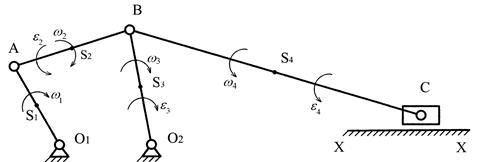
План
ускорений ![]()
3.
Силовой расчет механизма
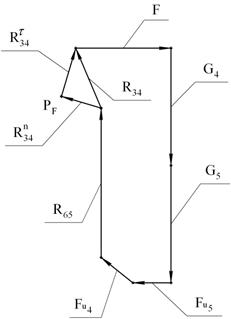
3.1. Силовой расчет
последней группы Ассура вида ВВП
3.1.1. Определение
сил тяжести звеньев:
![]() ,
, ![]()
3.1.2. Определение
сил инерции:
![]()
![]()
![]()
Силы инерции направлены в противоположную сторону
соответствующим ускорениям центров масс звеньев.
3.1.3. Определение
момента инерции:
![]() Нм;
Нм;
Момент инерции направлен в противоположную сторону
угловому ускорению![]() .
.
Построим группу Ассура в масштабе![]() .
.
Покажем все действующие на нее силы и неизвестные
реакции ![]() .
.
3.1.4. Определим
реакцию![]() :
:
Составим уравнение моментов всех сил, действующих на звено 4, относительно точки С.
![]() .
.
Найдем реакцию ![]() .
.
![]()
Длины плеч h1 и h2 измерены на расчетной схеме и умножены на масштабный
коэффициент ![]() м/мм.
м/мм.
![]() м,
м, ![]() м.
м.
3.1.5. Определим
реакции ![]() и
и![]() :
:
Составим векторное уравнение равновесия всех сил,
действующих на всю группу Ассура.
![]() .
.
Выберем масштаб плана сил ![]() м/мм.
м/мм.
Вычислим величины отрезков, соответствующих векторам
сил. Данные занесем в табл. 1:
Таблица 1
|
Обозначение силы |
|
|
|
|
F |
|
|
|
|
|
|
Величина силы, Н |
49 |
49 |
17,25 |
16,25 |
40 |
20,5 |
17 |
27 |
62 |
27 |
|
Отрезок на плане, мм |
49 |
49 |
17 |
16 |
40 |
21 |
17 |
27 |
62 |
27 |
Строим план сил. В соответствии с
векторным уравнением откладываем отрезки, соответствующие векторам ![]() . Векторы можно откладывать в любом
порядке, но обязательно начать построение с вектора
. Векторы можно откладывать в любом
порядке, но обязательно начать построение с вектора ![]() . Затем из начала вектора
. Затем из начала вектора ![]() проводим направление вектора
проводим направление вектора ![]() , а из конца последнего вектора
проводим направление вектора
, а из конца последнего вектора
проводим направление вектора ![]() . Пересекаясь, эти направления
замыкают многоугольник сил.
. Пересекаясь, эти направления
замыкают многоугольник сил.
Измеряя на плане сил отрезки, соответствующие векторам
![]() ,
, ![]() ,
, ![]() и умножая их на масштаб
и умножая их на масштаб ![]() , получим значение этих реакций. Данные занесены в
табл. 1.
, получим значение этих реакций. Данные занесены в
табл. 1.
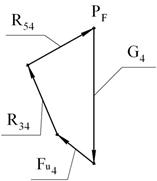
3.1.6. Определим
реакцию R54.
Составим векторное уравнение равновесия всех сил,
действующих звено 4.
![]() .
.
Выберем масштаб плана сил ![]() м/мм.
м/мм.
Строим план сил. В соответствии с векторным уравнением
откладываем отрезки, соответствующие векторам ![]() . Векторы можно откладывать в любом порядке. Соединяя
начало первого вектора и конец последнего, получим многоугольник сил и отрезок,
определяющий реакцию
. Векторы можно откладывать в любом порядке. Соединяя
начало первого вектора и конец последнего, получим многоугольник сил и отрезок,
определяющий реакцию ![]() . Измеряя его длину и умножая на масштаб
. Измеряя его длину и умножая на масштаб![]() , получим величину реакции
, получим величину реакции ![]() .
.
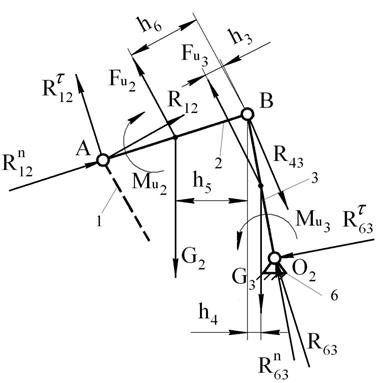
3.2. Силовой расчет
предпоследней группы Ассура вида ВВВ.
3.2.1. Определение
сил тяжести звеньев:
![]()
![]()
3.2.2. Определение
сил инерции:
![]() ,
, ![]()
![]()
Силы инерции направлены в противоположную сторону
соответствующим ускорениям центров масс звеньев.
3.2.3. Определение
моментов инерции:
![]()
![]()
Моменты инерции направлены в противоположные стороны
соответствующим угловым ускорениям.
Построим группу Ассура в масштабе ![]() .
.
Покажем все действующие на нее силы (в том числе
реакцию ![]() ) и неизвестные реакции
) и неизвестные реакции ![]() .
.
3.2.4. Определим
реакцию ![]() .
.
Составим уравнение моментов всех сил, действующих на звено 2, относительно точки В.
![]() .
.
Найдем реакцию![]() :
:
![]()
Длины плеч h5
и h6 измерены на расчетной
схеме и умножены на масштабный коэффициент ![]() м/мм.
м/мм.
![]() м,
м, ![]() м.
м.
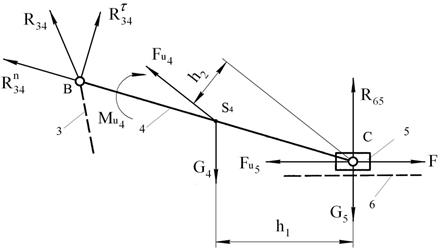
Последняя группа
Ассура вида ВВП ![]() м/мм
м/мм
|
План сил для группы Ассура
|
План сил для звена 4 |
|
|
|
3.2.5. Определим
реакцию ![]() .
.
Составим уравнение моментов всех сил, действующих на звено 3, относительно точки В.
![]() .
.
Найдем реакцию ![]() .
.
![]()
Длины плеч h3
и h4 измерены на
расчетной схеме и умножены на масштабный коэффициент ![]() м/мм.
м/мм.
![]() м,
м, ![]() м.
м.
3.2.6. Определим
реакции ![]() и
и![]() .
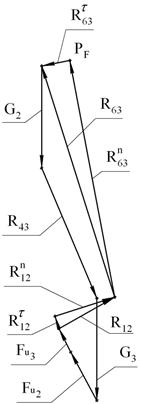
.
Составим векторное уравнение равновесия всех сил,
действующих на всю группу Ассура.
![]() .
.
Выберем масштаб плана сил ![]() м/мм.
м/мм.
Вычислим величины отрезков, соответствующих векторам
сил. Данные занесем в табл. 2.
Строим план сил. В соответствии с
векторным уравнением откладываем отрезки, соответствующие векторам ![]() . Векторы можно откладывать в любом
порядке, но обязательно начать построение с вектора
. Векторы можно откладывать в любом
порядке, но обязательно начать построение с вектора ![]() , а закончить построение вектором
, а закончить построение вектором ![]() . Затем из начала вектора
. Затем из начала вектора ![]() проводим направление вектора
проводим направление вектора ![]() , а из конца вектора
, а из конца вектора ![]() проводим направление вектора
проводим направление вектора ![]() . Пересекаясь, эти направления замыкают
многоугольник сил. Измеряя на
плане сил отрезки, соответствующие векторам
. Пересекаясь, эти направления замыкают
многоугольник сил. Измеряя на
плане сил отрезки, соответствующие векторам ![]() и умножая их на
масштаб
и умножая их на
масштаб![]() , получим значение этих реакций. Данные занесены в
табл. 2.
, получим значение этих реакций. Данные занесены в
табл. 2.
Таблица 2
|
Обозначение силы |
|
|
|
|
|
|
|
|
|
|
|
|
Величина силы,
Н |
19,6 |
19,6 |
10,7 |
4,8 |
27 |
12,5 |
2,66 |
12 |
46,5 |
5,56 |
46 |
|
Отрезок
на плане,
мм |
39 |
39 |
21 |
10 |
54 |
25 |
5 |
24 |
93 |
11 |
92 |
|
Предпоследняя группа Ассура вида ВВВ |
План сил для группы Ассура |
|
|
|
3.3.
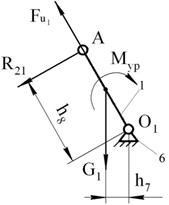
Силовой расчет начального механизма
3.3.1 .Определение
силы тяжести звена:
![]()
3.3.2. Определение
силы инерции:
![]()
Сила инерции направлена в противоположную сторону
ускорению![]() .
.
Построим начальный механизм в масштабе![]() .
.
Покажем все действующие на него силы, неизвестную
реакцию ![]() и
уравновешивающий момент Mур.
и
уравновешивающий момент Mур.
3.3.3. Найдем
величину уравновешивающего момента
Mур.
Запишем уравнение моментов всех сил относительно точки
О1.
![]() .
.
Уравновешивающий момент Mур равен:
![]()
Здесь ![]() .
.
Длины плеч h7
и h8 измерены на расчетной
схеме и умножены на масштабный коэффициент ![]() м/мм.
м/мм.
![]() м,
м, ![]() м.
м.
Тогда уравновешивающая сила равна:
![]()
3.3.4. Найдем реакцию
R61.
Составим векторное уравнение равновесия всех сил, действующих
на начальный механизм.
![]() .
.
Выберем масштаб плана сил ![]() м/мм.
м/мм.
Вычислим величины отрезков, соответствующих векторам
сил. Данные занесем в табл. 3:
Таблица 3
|
Обозначение силы |
|
|
|
|
|
Величина силы, Н |
14,7 |
4,43 |
12,5 |
21,5 |
|
Отрезок
на плане, мм |
29 |
9 |
25 |
43 |
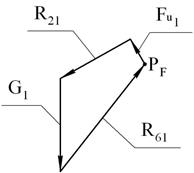
Строим план сил. В соответствии с векторным уравнением
откладываем отрезки, соответствующие векторам ![]() . Векторы можно откладывать в любом порядке. Соединяя
начало первого вектора и конец последнего, получим многоугольник сил и отрезок,
определяющий реакцию
. Векторы можно откладывать в любом порядке. Соединяя
начало первого вектора и конец последнего, получим многоугольник сил и отрезок,
определяющий реакцию ![]() . Измеряя его длину и умножая на масштаб μF, получим величину реакции
. Измеряя его длину и умножая на масштаб μF, получим величину реакции ![]() . Данные занесены в табл. 3.
. Данные занесены в табл. 3.
|
Начальный механизм |
План сил для начального механизма |
|
|
|
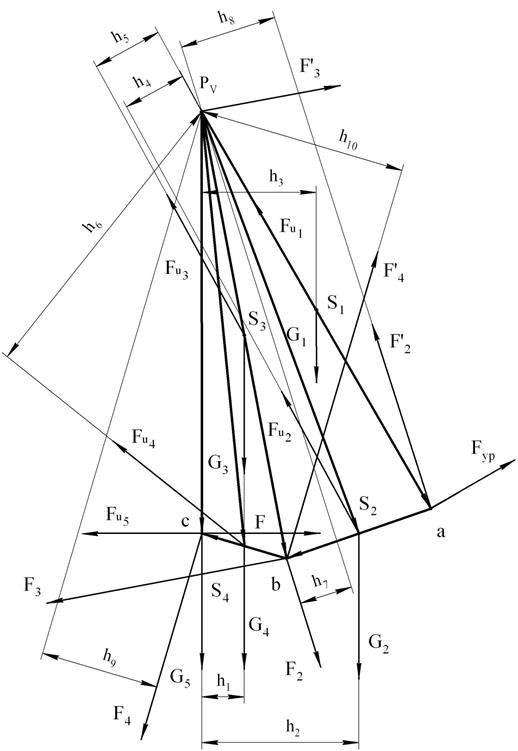
4. Определение уравновешивающей силы с
помощью рычага Жуковского Н.Е.
4.1. Уравновешивающую силу Fур приложим в точке А перпендикулярно кривошипу О1А.
4.2. План скоростей повернем на 90°.
В
соответствующих точках плана скоростей приложим векторы сил, сохраняя их
направления, каждый момент инерции ![]() заменим парой
сил. Силы проводятся из кинематических пар звена под углом 90º так, чтобы
эти силы вращали звено в ту же сторону, что и соответствующий момент инерции:
заменим парой
сил. Силы проводятся из кинематических пар звена под углом 90º так, чтобы
эти силы вращали звено в ту же сторону, что и соответствующий момент инерции:
![]()
![]()
![]()
и каждую силу перенесем на план.
4.3
.Составим уравнение моментов всех сил относительно полюса pv:
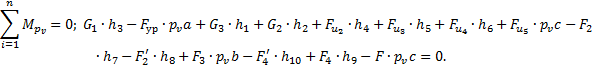
Решая уравнение, получим:
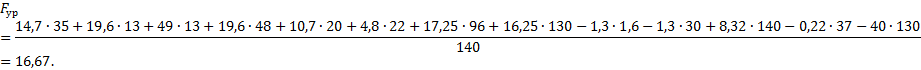
Длины
всех плеч измерены на расчетной схеме.
Таким образом, с помощью теоремы
Жуковского Н.Е можно:
1.
Определить уравновешивающую силу ![]() , не проводя силового расчета;
, не проводя силового расчета;
2.
Проверить значение уравновешивающей силы ![]() , полученной из силового расчета. Погрешность расчетов
составляет:
, полученной из силового расчета. Погрешность расчетов
составляет:
![]()
Погрешность
не должна превышать 20%.
Рычаг Жуковского ![]()
Приложение. Основные формулы для определения скоростей
и ускорений точек звеньев
|
№ |
Вид движения |
Скорость |
Ускорение |
|
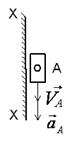
1 |
Поступательное (ползун по стойке)
|
Все точки звена имеют
одинаковую скорость
|
Все точки звена имеют одинаковые
ускорения
|
|
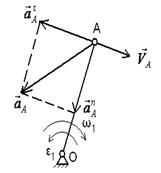
2 |
Вращательное вокруг неподвижной оси (кривошип или коромысло
относительно стойки)
|
Скорость точки А
Вектор
|
Полное ускорение точки А
Нормальное ускорение Вектор
Касательное ускорение Вектор
|
|
3 |
Звено совершает плоскопараллельное
движение (шатун)
|
Скорость точки В
Относительная скорость
Вектор
|
Ускорение точки В
Относительное ускорение
Нормальное ускорение
Вектор
Касательное ускорение
Вектор
|
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов